viernes, 25 de abril de 2014
martes, 15 de abril de 2014
Propiedades de los Numeros Reales
9:50
No comments
Las propiedades de los nuemros reales son las mismas que las propiedades de los números enteros, racionales y irracionales donde se cumple que:
Propiedades de densidad y completitud
Si dividimos el intervalo 36-37 en diez partes iguales y obtenemos nuevos números, dividimos el intervalo 36, 5- 36,6 en diez partes iguales y se obtiene nuevos números. En consecuencia si seguimos dividiendo y ampliando cada parte y siempre obtendremos nuevos números. observamos que entre dos números reales, existe infinitos números reales; además cada punto de la recta numérica le corresponde un único numero real diferente.
El conjunto de nuemros reales es denso porque entre cada par de números existe y se puede representar infinitos números; y es completo porque cada punto de la recta se corresponde con un numero real. veamos un vídeo.
El Conjunto de Números Reales(R)
8:55
No comments
El Conjunto de Números Reales
El conjunto de los números reales (R) es la unión del conjunto de los números relacionales e irracionales:

El conjunto de los números racionales (Q) está formado por todas las fracciones o expresiones decimales finitas o infinitas periódicas puras o mixtas, como:

El conjunto de Numero Enteros y Naturales, se consideran como números racionales como podemos ver en el siguiente gráfico:
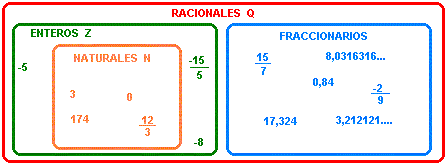
de igual forma, El conjunto de números Irracionales (I) esta formado por todos los decimales infinitos no periódicos, aquí están los números radicales, el PI π = 3.14159265359..,


En consecuencia se deduce, que el conjunto de números reales, es el conjunto que contiene a los raciones y los irracionales como:
















